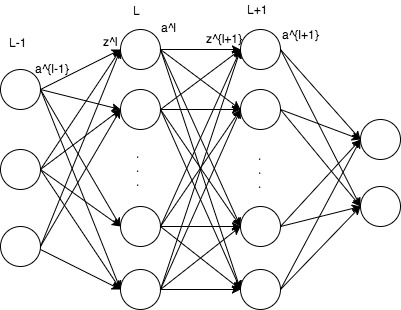
假设有m个样本\((x_1,y_1), (x_2, y_2),...(x_m,y_m)\), 对于其中一个样本\((x,y)\),其平方损失函数如下:
\[J(W,b,x,y)= \frac{1}{2} \Vert{h_{W,b}(x)-y}\Vert^2\]第l层和第l+1层之间的前向传播:
\[z^{l+1}=W^la^l+b^l \\ a^{l+1}=f(z^{l+1})\]假设损失函数为平方损失,使用L2正则,神经网络层数为\(n_l\),第l层的神经元个数为\(s_l\), 此时整体平方损失函数:
\[\begin{align*} J(w,b)&=\left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^i,y^i) \right] + \frac{\lambda}{2}\sum_{l=1}^{n_l-1}\sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}}(W_{ji}^l)^2 \\ &= \left[ \frac{1}{m} \sum_{i=1}^m \frac{1}{2} \Vert{h_{W,b}(x^i)-y^i}\Vert^2 \right] + \frac{\lambda}{2}\sum_{l=1}^{n_l-1}\sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}}(W_{ji}^l)^2 \end{align*}\]偏导如下:
\[\frac{\partial}{\partial W_{ij}^l}J(W,b) = \left[\frac{1}{m} \sum_{i=1}^m \frac{\partial} {\partial W_{ij}^l } J(W,b; x^i, y^i) \right] + \lambda W_{ij}^l \\ \frac{\partial}{\partial b_{i}^l}J(W,b)=\frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial b_i^l}J(W,b; x^i, y^i)\]第\(n_l\)层(最后一层)第i个单元的残差如下:
\[\begin{align*} \delta_i^{n_l}&=\frac{\partial}{\partial z_i^{n_l} } J(W,b;x,y) \\ &=\frac{\partial}{\partial z_i^{n_l} } \frac{1}{2} \Vert y- h_{W,b}(x)\Vert^2 \\ &= \frac{\partial}{\partial z_i^{n_l} }\frac{1}{2}\sum_{j=1}^{S_{n_l}} (y_j-a_j^{n_l})^2 \\ &=\frac{\partial}{\partial z_i^{n_l} }\frac{1}{2}\sum_{j=1}^{S_{n_l}} (y_j-f(z_j^{n_l}))^2 \\ &=-(y_i-f(z_i^{n_l}))f'(z_i^{n_l}) \\ &= -(y_i -a_i^{n_l})f'(z_i^{n_l}) \end{align*}\]即预估值和真实值之间的残差(损失函数和输出层的输出之间的梯度)和激活函数的梯度之间的乘积。
第\(n_{l-1}\)层第i个单元的残差如下:
\[\begin{align*} \delta_i^{n_l-1} &= \frac{\partial}{\partial z_i^{n_l-1} } J(W,b;x,y) \\ &=\frac{\partial}{\partial z_i^{n_l-1} } \frac{1}{2} \Vert y-h_{W,b}(x)\Vert^2 \\ &=\frac{\partial}{\partial z_i^{n_l-1} } \frac{1}{2} \sum_{j=1}^{S_{n_l}} (y_j-a_j^{n_l})^2 \\ &= \frac{1}{2}\sum_{j=1}^{S_{n_l}} \frac{\partial}{\partial z_i^{n_l-1}}(y_j-a_j^{n_l})^2 \\ &= \frac{1}{2}\sum_{j=1}^{S_{n_l}} \frac{\partial}{\partial z_i^{n_l-1}}(y_j-f(z_j^{n_l}))^2 \\ &= \sum_{j=1}^{S_{n_l}} -(y_j-f(z_j^{n_l})) \frac{\partial f(z_j^{n_l}) }{\partial z_i^{n_l-1}} \\ &= \sum_{j=1}^{S_{n_l}} -(y_j-f(z_j^{n_l})) f'(z_j^{n_l}) \frac{\partial z_j^{n_l} }{\partial z_i^{n_l-1}} \\ &= \sum_{j=1}^{S_{n_l}} \delta_j^{n_l} \frac{\partial z_j^{n_l} }{\partial z_i^{n_l-1}} \\ &= \sum_{j=1}^{S_{n_l}}\left( \delta_j^{n_l} \frac{\partial }{\partial z_i^{n_l-1}} \sum_{k=1}^{S_{n_l-1} } f(z_k^{n_l-1}) W_{jk}^{n_l-1} \right) \\ &= \sum_{j=1}^{S_{n_l}}\left( \delta_j^{n_l} W_{ji}^{n_l-1} f'(z_i^{n_l-1}) \right) \\ &= \sum_{j=1}^{S_{n_l}}\left( \delta_j^{n_l} W_{ji}^{n_l-1} \right) f'(z_i^{n_l-1}) \end{align*}\]即前一层的每个节点的残差和前一层的节点和当前节点之间的边的对应的权重的乘积再乘上隐层激活函数的梯度。
最终推导如下:
\[\frac{\partial}{\partial W_{ij}^l}J(w,b;x,y) = a_j^l\delta_i^{l+1} \\ \frac{\partial}{\partial b_{i}^l}J(w,b;x,y) = \delta_i^{l+1} \\\]