假设有m个样本\((x_1,y_1), (x_2, y_2),...(x_m,y_m)\).
对于其中一个样本\((x,y)\),其t时刻的平方损失函数如下:
\[J(x,y)= \frac{1}{2} \Vert{y^t-y}\Vert^2\]RNN推导
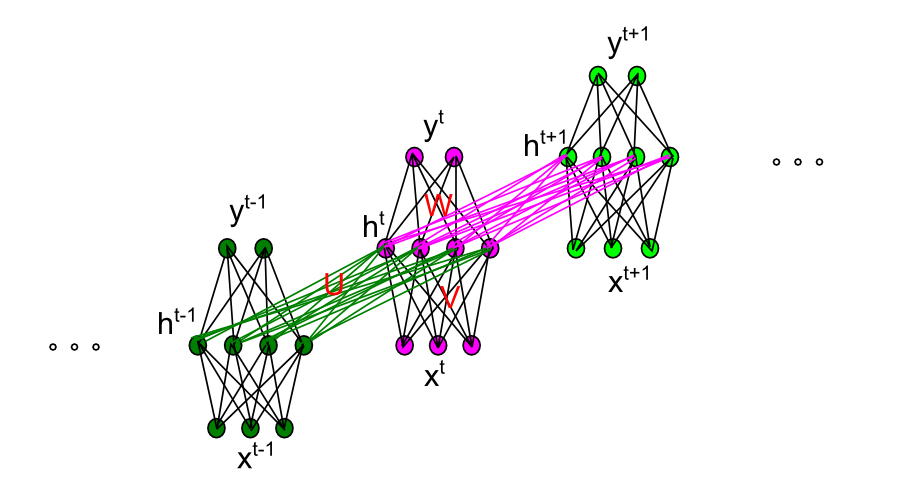
前向传播:
\[\begin{align} z_h^t & = x^tV + h^{t-1}U + b_h \\ h^t & = f(z_h^t) \\ z_y^t & = h^tW + b_y \\ y^t & = g(z_y^t) \\ \end{align}\]其中,\(f\)我们可以使用sigmoid函数。
需要进行求解的参数包括\(U,V,W\)和\(b_h, b_y\). \(U\)表示和隐藏层和隐藏层之间的权重矩阵,\(V\)表示输入层与隐藏层之间的连接矩阵,\(W\)表示隐藏层和输出层之间的权重矩阵.
下面对各个参数求导
\[\begin{align} \frac{\partial E} {\partial W_{jk}} &= \frac{\partial E} {\partial z_{yk}^t} \frac{\partial z_{yk}^t} {\partial W_{jk} } \\ &= \frac{\partial E} {\partial z_{yk}^t} h_j^t \\ &= \frac{\partial E} {\partial y_k^t} \frac{\partial y_k^t }{\partial z_{yk}^t}h_j^t \\ &= (y_k^t - d_k^t)y^t_k(1-y^t_k)h_j^t \\ \end{align}\] \[\begin{align*} \frac{\partial E} {\partial V_{ij}} &= \frac{\partial E} {\partial z^t_{hj}} \frac{\partial z^t_{hj}} {\partial V_{ij}} \\ &= \frac{\partial E} {\partial z^t_{hj}} x^t_i \\ &= (\sum_k \frac{\partial E}{\partial z^t_{yk}} \frac{\partial z^t_{yk}}{\partial h^t_j} \frac{\partial h^t_j}{\partial z^t_{hj}} + \color{red}{ \sum_r \frac{\partial E}{\partial z^{t+1}_{hr}} \frac{\partial z^{t+1}_{hr}}{\partial h^{t}_{j}} \frac{\partial h^{t}_{j}} {\partial z^t_{hj}} })x^t_i \\ &= (\sum_k \frac{\partial E}{\partial z^t_{yk}} W_{jk} + \color{red} { \sum_r \frac{\partial E}{\partial z^{t+1}_{hr}}U_{jr}} ) \frac{\partial h^{t}_{j}} {\partial z^t_{hj}} x^t_i \\ \end{align*}\] \[\begin{align} \frac{\partial E} {\partial U_{jr}} &= \frac{\partial E} {\partial z^{t}_{hr}} \frac{\partial z^{t}_{hr}}{\partial U_{jr}} \\ &= \frac{\partial E}{\partial z^{t}_{hr}} h^{t-1}_j \\ &= (\sum_k \frac{\partial E} {\partial z^{t}_{yk}} \frac {\partial z^{t}_{yk}} {\partial h^{t}_r} \frac {\partial h^{t}_r} {\partial z^{t}_{hr}} + \color{red}{\sum_j \frac{\partial E} {\partial z^{t+1}_{hj}} \frac {\partial z^{t+1}_{hj}} {\partial h^{t}_r} \frac {\partial h^{t}_r} {\partial z^{t}_{hr}}}) h^{t-1}_j \\ &= (\sum_k \frac{\partial E} {\partial z^{t}_{yk}} W_{rk} + \color{red}{\sum_l \frac{\partial E} {\partial z^{t+1}_{hl}} U_{lr}}) \frac {\partial h^{t}_r} {\partial z^{t}_{hr}} h^{t-1}_j \\ \end{align}\]令\(\delta_{y,k}^t\)表示t时刻输出层第k个神经元的误差项,\(\delta_{h,j}^t\)为t时刻隐含层第j 个神经元的误差项.
\[\begin{align} \delta_{y,k}^t &= \frac{\partial E} {\partial z_{yk}^t} \\ &= (y_k^t - d_k^t)y^t_k(1-y^t_k) \\ \end{align}\] \[\begin{align} \delta_{h,j}^t &= \frac{\partial E} {\partial z_{hj}^t} \\ &= (\sum_k \frac{\partial E}{\partial z^t_{yk}} W_{jk} + \sum_r \frac{\partial E}{\partial z^{t+1}_{hr}}U_{jr}) \frac{\partial h^{t}_{j}} {\partial z^t_{hj}} \\ &= (\sum_k \delta_{y,k}^t W_{jk} + \sum_r \delta_{h,j}^{t+1} U_{jr}) \frac{\partial h^{t}_{j}} {\partial z^t_{hr}} \end{align}\]则有:
\[\begin{align} \frac{\partial E} {\partial W_{jk}} & = \delta_{y,k}^t h_j^t \\ \frac{\partial E} {\partial V_{ij}} & = \delta_{h,j}^t x^t_i \\ \frac{\partial E} {\partial U_{jr}} & = \delta_{h,r}^t h^{t-1}_j \\ \end{align}\]LSTM推导
 前向传播
前向传播
反向传播
令输出层、输入门、输出门、遗忘门、cell的误差项分别为\(\delta_y^t,\delta_i^t,\delta_o^t,\delta_f^t,\delta_c^t\)。
\[\begin{align} \delta_y^t & = \frac{\partial E} {\partial z_y^t} \\ \delta_i^t & = \frac{\partial E} {\partial z_i^t} \\ \delta_f^t & = \frac{\partial E} {\partial z_f^t} \\ \delta_o^t & = \frac{\partial E} {\partial z_o^t} \\ \delta_c^t & = \frac{\partial E} {\partial z_c^t} \\ \end{align}\]首先,定义两个中间变量:
\[\begin{align} \epsilon^t_h &= \frac{\partial E} {\partial h^t} \\ &= \frac{\partial E} {\partial z_y^t} \cdot \frac{\partial z_y^t} {\partial h^t} + \frac{\partial E} {\partial z_i^{t+1}} \frac{\partial z_i^{t+1}} { \partial h^t } + \frac{\partial E} {\partial z_f^{t+1}} \frac{\partial z_f^{t+1}} { \partial h^t } +\frac{\partial E} {\partial z_o^{t+1}} \frac{\partial z_o^{t+1}} { \partial h^t } + \frac{\partial E} {\partial z_c^{t+1}} \frac{\partial z_c^{t+1}} { \partial h^t } \\ &= \delta_y^t \cdot (w_y)^T + \delta_i^{t+1}\cdot (w_{ih})^T + \delta_f^{t+1}\cdot (w_{fh})^T + \delta_o^{t+1}\cdot (w_{oh})^T + \delta_c^{t+1}\cdot (w_{ch})^T \\ \epsilon^t_c &= \frac{\partial E} {\partial c^t} \\ &= \frac{\partial E} {\partial h^t} \cdot \frac{\partial h^t} {\partial c^t} + \frac{\partial E} {\partial c^{t+1}} \cdot \frac{\partial c^{t+1}} {\partial c^{t}} \\ &= \epsilon^t_h \cdot o^t \cdot h'(c^t) + \epsilon^{t+1}_c \cdot f^{t+1} \end{align}\]各个门的误差项如下:
\[\begin{align} \delta_y^t & = \frac{\partial E} {\partial z_y^t} = \frac{\partial E}{\partial y^t} \cdot \frac{\partial y^t}{\partial z_y^t} \\ & = (y^t - d^t) \cdot g'(z_y^t) \\ \delta_i^t & = \frac{\partial E} {\partial z_i^t} = \frac{\partial E} {\partial i^t} \cdot \frac{\partial i^t} {\partial z_i^t} \\ & = \frac{\partial E} {\partial c^t} \cdot \frac{\partial c^t} {\partial i^t} \cdot g'(z_i^t) \\ & = \epsilon^t_c \cdot \tilde{c}^t \cdot g'(z_i^t) \\ \delta_f^t & = \frac{\partial E} {\partial z_f^t} = \frac{\partial E} {\partial f^t} \cdot \frac {\partial f^t} {\partial z_f^t} \\ & = \frac{\partial E} {\partial c^t} \cdot \frac{\partial c^t} {\partial f^t} \cdot g'(z_f^t)\\ & = \epsilon^t_c \cdot c^{t-1} \cdot g'(z_f^t) \\ \delta_o^t & = \frac{\partial E} {\partial z_o^t} = \frac{\partial E} {\partial o^t} \cdot \frac {\partial o^t} {\partial z_o^t} \\ & = \frac{\partial E} {\partial h^t} \cdot \frac{\partial h^t} {\partial o^t} \cdot g'(z_o^t)\\ & = \epsilon^t_h \cdot h(c^t) \cdot g'(z_o^t) \\ \delta_c^t & = \frac{\partial E} {\partial z_c^t} =\frac{\partial E} {\partial \tilde{c}^t} \cdot \frac {\partial \tilde{c}^t} {\partial z_c^t} \\ & = \frac{\partial E} {\partial c^t} \cdot \frac{\partial c^t} {\partial \tilde{c}^t} \cdot g'(z_c^t)\\ &= \epsilon^t_c \cdot i^t \cdot g'(z_c^t) \end{align}\]各个参数的梯度如下:
\[\begin{align} \frac{ \partial E} { \partial w_{ix} } &= \frac{ \partial E} { \partial z_i^t } \frac{ \partial z_i^t } { \partial w_{ix}} = (x^t)^T \delta_i^t \\ \frac{ \partial E} { \partial w_{ih} } &= \frac{ \partial E} { \partial z_i^t } \frac{ \partial z_i^t } { \partial w_{ih}} = (h^{t-1})^T \delta_i^t \\ \frac{ \partial E} { \partial w_{fx} } &= \frac{ \partial E} { \partial z_f^t } \frac{ \partial z_f^t } { \partial w_{fx}} = (x^t)^T \delta_f^t \\ \frac{ \partial E} { \partial w_{fh} } &= \frac{ \partial E} { \partial z_f^t } \frac{ \partial z_f^t } { \partial w_{fh}} = (h^{t-1})^T \delta_f^t \\ \frac{ \partial E} { \partial w_{ox} } &= \frac{ \partial E} { \partial z_o^t } \frac{ \partial z_o^t } { \partial w_{ox}} = (x^t)^T \delta_o^t \\ \frac{ \partial E} { \partial w_{oh} } &= \frac{ \partial E} { \partial z_o^t } \frac{ \partial z_o^t } { \partial w_{oh}} = (h^{t-1})^T \delta_o^t \\ \frac{ \partial E} { \partial w_{cx} } &= \frac{ \partial E} { \partial z_c^t } \frac{ \partial z_c^t } { \partial w_{cx}} = (x^t)^T \delta_c^t \\ \frac{ \partial E} { \partial w_{ch} } &= \frac{ \partial E} { \partial z_c^t } \frac{ \partial z_c^t } { \partial w_{ch}} = (h^{t-1})^T \delta_c^t \\ \frac{ \partial E} { \partial w_{y} } &= \frac{ \partial E} { \partial z_y^t } \frac{ \partial z_y^t } { \partial w_{y}} = (h^{t})^T \delta_y^t \\ \end{align}\]GRU推导
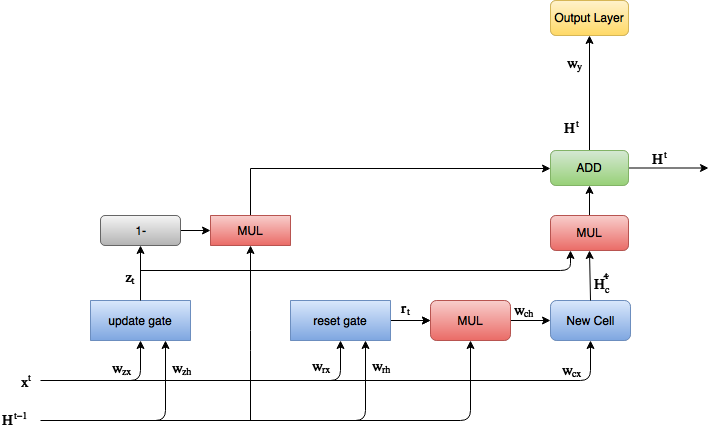
前向传播
\[\begin{align} z^t & = \sigma( w_{zx} x^t + w_{zh} H^{t-1}) \\ r^t & = \sigma( w_{rx} x^t + w_{rh} H^{t-1}) \\ \tilde{H_c^{t}} & = h( W_{cx} X^t + W_{ch} r^t * H^{t-1} ) \\ H^t & = (1-z^t) * H^{t-1} + z^t * \tilde{H_c^{t}} \\ z_y^t &= H^t w_y \\ y^t &= g(z_y^t) \end{align}\]后向传播
\[\begin{align} \delta_y^t &= \frac{\partial E} {\partial z_y^t} = \frac{\partial E}{\partial y^t} \cdot \frac{\partial y^t}{\partial z_y^t} \\ & = (y^t - d^t) \cdot g'(z_y^t) \\ \delta_z^t &= \frac{\partial E} {\partial z_z^t} = \frac{\partial E}{\partial H^t} \frac{\partial H^t } { \partial z^t} \frac{ \partial z^t} { \partial z_z^t} \\ \delta_r^t &= \frac{\partial E} {\partial z_r^t }= \frac{ \partial E} { \partial H^t} \frac{\partial H^t} { \partial \tilde{H_c^t} } \frac{ \partial \tilde{H_c^t} }{\partial z_c^t} \frac{ \partial z_c^t } {\partial r^t } \frac { \partial r^t } { \partial z_r^t }\\ \delta_c^t &= \frac{\partial E } {\partial z_c^t } = \frac { \partial E} {\partial H^t } \frac { \partial H^t} { \partial \tilde{H_c^t} }\frac{ \partial \tilde{H_c^t} }{ \partial z_c^t } \end{align}\] \[\begin{align} \frac{\partial E} {\partial H^t} = \frac{\partial E}{\partial y_t }\frac{ \partial y_t } { \partial H^t } + \frac{\partial E } { \partial z^{t+1} } \frac{ \partial z^{t+1} } { \partial H^t } + \frac{\partial E } { \partial r^{t+1} } \frac{ \partial r^{t+1} } { \partial H^t } + \frac{\partial E } { \partial c^{t+1} } \frac{ \partial c^{t+1} } { \partial H^t } + \frac{ \partial E } { \partial H^{t+1} } \frac{ \partial H^{t+1} } { \partial H^t } \end{align}\]各项参数的梯度如下:
\[\begin{align} \frac{ \partial E} { \partial w_{zx} } &= \frac{ \partial E} { \partial z_z^t } \frac{ \partial z_z^t } { \partial w_{zx} } \\ \frac{ \partial E} { \partial w_{zh} } &= \frac{ \partial E} { \partial z_z^t } \frac{ \partial z_z^t } { \partial w_{zh} } \\ \frac{ \partial E} { \partial w_{rx} } &= \frac{ \partial E} { \partial z_r^t } \frac{ \partial z_r^t } { \partial w_{rx} } \\ \frac{ \partial E} { \partial w_{rh} } &= \frac{ \partial E} { \partial z_r^t } \frac{ \partial z_r^t } { \partial w_{rh} } \\ \frac{ \partial E} { \partial w_{cx} } &= \frac{ \partial E} { \partial z_c^t } \frac{ \partial z_c^t } { \partial w_{cx} } \\ \frac{ \partial E} { \partial w_{ch} } &= \frac{ \partial E} { \partial z_c^t } \frac{ \partial z_c^t } { \partial w_{ch} } \\ \end{align}\]