本文是对cs231中优化部分的简略笔记
Learning
前面讲了神经网络的静态部分:如何建立起神经网络的连接、数据和损失函数,本节讲解参数的学习过程
Gradient Checks
梯度检查其实就是比较梯度的解析解(analytic gradient)和数值解(numerical gradient)。这个过程比较复杂且容易出错。本文介绍了一些tips/tricks和需要注意的问题
Use the centered formula
计算梯度的数值解时你看到的是下面的优先差分近似公式( finite difference approximation )
\[\frac{df(x)}{dx} = \frac{f(x + h) - f(x)}{h} \hspace{0.1in} \text{(bad, do not use)}\]这个公式不好,以后不要用
h一般比较小,设置成1e-5差不多了
在实践中,一般使用中心差分g公式( centered difference formula )
\[\frac{df(x)}{dx} = \frac{f(x + h) - f(x - h)}{2h} \hspace{0.1in} \text{(use instead)}\]这个公式需要对x的每个维度都计算两次损失函数来检查梯度,但是这种方法可以证明会更精确。可以通过\(f(x+h\)和\(f(x-h\)的Talyor 展开式来z证明第一个公式的误差在\(O(h)\)量级,第二个公式的误差在\(O(h^2\)
Use relative error for the comparison
怎么才能知道梯度的数值解和解析解比较相近的?我们可能很自然的比较\(\mid f’_a - f’_n \mid\)的值或者对应的平方值,如果大于一定阈值就认为二者不相等。但是这种方法是有问题的。 比如误差是1e-4,如果梯度值在1.0左右时,这个差距看起来比较小,我们认为这两个值是相等的。 但是如果梯度在1e-5或者更低,那么误差为1e-4就是一个非常大的误差,此时我们认为计算是有问题的。所以检查相对误差会更合理:
\[\frac{\mid f'_a - f'_n \mid}{\max(\mid f'_a \mid, \mid f'_n \mid)}\]相对误差考虑了二者之间的差值和梯度的绝对值之间的比例。
相对误差有下面几条指导性的建议
1.相对误差大于1e-2通常意味这计算出错 2.相对误差在(1e-4,1e-2)区间你可能就要怀疑自己的计算是否出错了 3.相对误差小于1e-4对于带有kink的目标函数来说通常还ok,如果没有kinks(使用tanh作为激活函数和softmax),1e-4可能就太高了 4.1e-7或者更低通常意味着计算是正确的
kinks是指函数中存在不可导的点
记住,网络越深,相对误差会越高。所有如果你对一个10层的网络进行梯度检查,那么相对误差在1e-2可能还ok,因为误差是一路累积的。相反,如果对一个可微函数的梯度相对误差在1e-2就不可接受了。
Use double precision
常见的错误是单精度浮点数来进行梯度检查。有时候即使实现正确,单精度浮点数可能也会得到1e-2的相对误差值。
Stick around active range of floating point
阅读“What Every Computer Scientist Should Know About Floating-Point Arithmetic”
比如,在一个batch上对损失函数进行归一化,如果每个样本的梯度都很小,那么又除以了样本的个数,那么得到的梯度值就更小了,这样反过来又会导致更多的数值问题。这也是我喜欢打印出原始的数值解和解析解,确定比较的两个值不是非常小的值,通常绝对值在1e-10或者更小你就要注意了。这时你可能需要放大你的损失函数的值到一个更合理的范围。在这个范围里浮点数更加稠密(大概是说0少一些),比较理想的值是量级在1.0上,即浮点数的指数部分为0.
Kinks in the objective
目标函数中的不可导点
梯度检查中 不准确的一个来源就是kinks。 kinks是指目标函数中不可导的点。比如ReLU(max(0,x)),或者SVM损失,Maxout 神经元。考虑当x=-1e-6时,对ReLU函数进行梯度检查.既然x<0,那么这个点的梯度解析解就是0.但是计算出来的数值解可能就是一个非零值,因为f(x+h)可能会跨过kinks(h>1e-6),这时候梯度就非0了。你可能会觉得这是一个病态的例子,但是实际上这种例子很常见。
Use only few datapoints
解决kink带来的问题的一个方法就是使用更少的样本。因为带有kink的损失函数在样本越少时kinks越少,所以在你进行有限差分近似时遇到kink的可能性就越低。
Be careful with the step size h
不一定越少越好,因为h很小时会有数值准确度的问题。
Gradcheck during a “characteristic” mode of operation
我们需要认识到梯度检验是在参数空间的一个特定的点上进行的。即使在那个点上检查通过了,也不能立马就能断定梯度实现正确了。另外,一个随机的初始化可能不是参数空间最优代表性的点,这可能导致进入某种病态的情况,即梯度看起来是正确实现了,实际上并没有。比如,如果权重初始值很小,SVM会给所有样本分配一个几乎等于0的值。梯度将会在所有的数据点上展现出某种模式。一个实现错误的梯度可能依然表现出这种模式,而且不能泛化到更具代表性的操作模式,比如在一些得分比另一些得分更大的情况下就不行。所以,安全起见,最好在经过一个预热的过程之后再进行梯度检验。即在预热过程中神经网络开始进行学习,在损失下降后开始进行梯度检验。第一次就进行检验的危险就在于这样可能会引入某些病态的边界情况,掩盖了错误的实现。
Don’t let the regularization overwhelm the data
通常损失函数包括数据损失和正则损失,需要注意的是正则损失可能淹没数据损失。此时损失主要来自正则损失(正则损失形式更简单)。这时可能就掩盖了错误的实现。所以一般推荐在梯度检验时关掉正则损失,首先只检查数据损失,然后再单独检查正则损失。单独检查正则损失时可以是修改代码,去掉其中数据损失的部分,也可以提高正则化强度,确认其效果在梯度检查中是无法忽略的,这样不正确的实现就会被观察到了。
Remember to turn off dropout/augmentations
梯度检查时去掉任何不确定性的措施,比如dropout,随机数据扩展等。否则在计算数值梯度时他们就会引入巨大的误差。不好的地方在于无法对这些部分进行梯度检验,而他们也有可能实现错误,从而使梯度计算出错。,一个更好的解决方案就是在计算f(x+h)和f(x-h)前强制增加一个特定的随机种子,在计算解析梯度时也同样如此。这样这些包含不确定因素的方法也就变成确定性的了。
Check only few dimensions
通常梯度可能有上百万维,此时,只能检查其中一部分纬度,假设其他维度实现是正确的。注意,确保每种不同的参数都被检查了其中几个维度,比如我们为了方便把几种参数合并成了一个向量,比如偏置可能只占向量的很小一部分,此时我们就不能随机选几维,一定要把这种情况考虑到,确保所有参数都收到了正确的梯度。
Before learning: sanity checks Tips/Tricks
Look for correct loss at chance performance
确保当用小的数值初始化参数时损失值是正确的。最好是先检查数据损失(data loss),比如,对于CIFAR-10数据集,使用softmax分类器时初始的损失函数值应该是2.302, 因为初始化时每个类的概率是0.1,softmax 损失是正确类别的概率的负的对数,即-ln(0.1)=2.302.对于The Weston Watkins SVM,我们期望所有的边界都被越过,因为每个类的分数都基本上为0,所以期望损失为9,因为每个错误类别的边界值是1,如果没看到这些损失值,那么初始化可能就有问题了。
increasing the regularization strength should increase the loss 为啥
Overfit a tiny subset of data.
最重要的一点,在全部训练集上进行训练之前,先在一个很小的数据集(20个样本?)上进行训练,并且确保损失能达到0.在进行实验时,最好把正则化损失设置为0,否则,这个会阻止损失为0,除非你在一个小数据集上通过了sanity check,否则,不值得在全部训练集上进行训练。另外,也需要注意即使你在小数据集上过拟合了,实现有可能还是错误的。比如,因为某些错误,数据点的特征是随机的,这样算法也可能对小数据进行过拟合,但是在整个数据集上跑算法的时候,就没有任何泛化能力。
Babysitting the learning process
在训练神经网络时,应该监控多个重要数值.数值输出的图表是观察训练进程的一扇窗口,是直观理解不同的超参数设置效果的工具,
在下面的图表中,x轴通常都是表示周期(epochs)单位,该单位衡量了在训练中每个样本数据都被观察过次数的期望(一个周期意味着每个样本数据都被观察过了一次)。相较于迭代次数(iterations),一般更倾向跟踪周期,这是因为迭代次数与数据的批尺寸(batchsize)有关,而批尺寸的设置又可以是任意的。
Loss function
训练过程中首先需要跟踪的就是损失函数,在前向过程中该值是在每个batch上进行计算的。
下图是损失函数随时间的变化,尤其是不同的形状说明了学习率设置的是否合理。
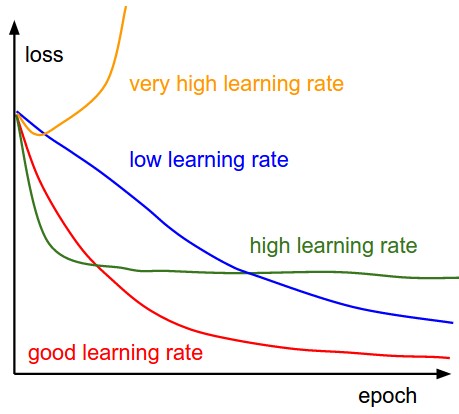
过低的学习率导致算法的改善是线性的。高一些的学习率会看起来呈几何指数下降,更高的学习率会让损失值很快下降,但是接着就停在一个不好的损失值上(绿线)。这是因为最优化的“能量”太大,参数在混沌中随机震荡,不能最优化到一个很好的点上。
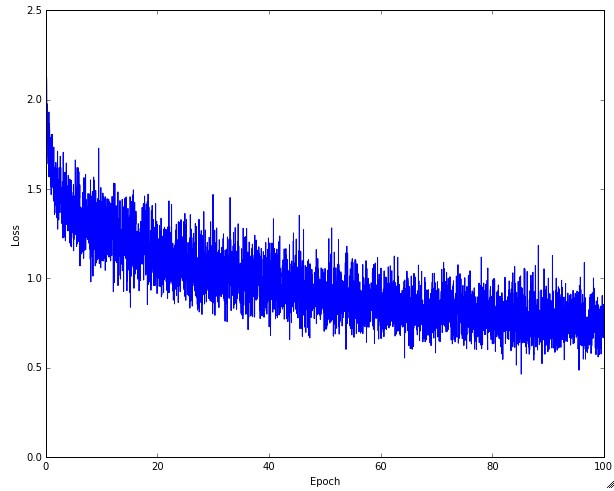
显示了一个典型的随时间变化的损失函数值,在CIFAR-10数据集上面训练了一个小的网络,这个损失函数值曲线看起来比较合理(虽然可能学习率有点小,但是很难说),而且指出了批数据的数量可能有点太小(因为损失值的噪音很大)。
损失值的震荡程度(wiggle)和批尺寸(batch size)有关,当批尺寸为1,震荡会相对较大。当批尺寸就是整个数据集时震荡就会最小,因为每个梯度更新都是单调地优化损失函数(除非学习率设置得过高)。
Train/Val accuracy
第二个需要跟踪的数值就是验证集和训练集的准确率,这个图可以帮你判断模型过拟合的程度。
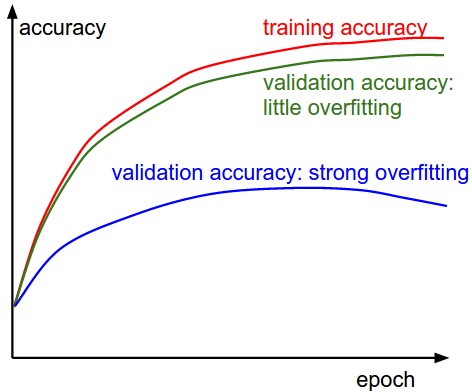
在训练集准确率和验证集准确率中间的空隙指明了模型过拟合的程度。在图中,蓝色的验证集曲线显示验证集的准确率比训练集低了很多,这说明模型有很强的过拟合。如果遇到这种情况,就应该增大正则化强度(更强的L2权重惩罚,更多的随机失活(dropout)等)或收集更多的数据。另一种可能就是验证集曲线和训练集曲线十分相近,这种情况说明你的模型容量(capacity)还不够大:应该通过增加参数数量让模型容量更大些。
Ratio of weights:updates
最后一个需要跟踪的数值是权重更新值和权重数值本身之间的比例。注意,是更新量,而不是原始梯度(比如,在普通sgd中就是梯度乘以学习率)。 你可能需要对每个参数跟踪和计算这个比例,一个经验性的结论是这个比例应该在1e-3左右。如果更低,说明学习率可能太小,如果更高,说明学习率可能太高。下面是具体例子:
# 假设参数向量为W,其梯度向量为dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # 简单SGD更新
update_scale = np.linalg.norm(update.ravel())
W += update # 实际更新
print update_scale / param_scale # 要得到1e-3左右
Activation / Gradient distributions per layer
不正确的初始化可能会减慢甚至使学习过程完全停止,幸运得是这个问题可以比较容易的检测出来,一种方法就是画出神经网络各层的激活函数和梯度的直方图。直观地说,如果看到任何奇怪的分布情况,那都不是好兆头.如果是tanh 神经元,我们期望看到激活函数分布在在(-1,1)之间,而不是全部都输出0,或者全部到饱和到-1或1。
First Layer Visualizations
最后,如果你处理的是图像的话,把第一层的特征可视化通常会有帮助。
Parameter updates
梯度解析解计算出来后,梯度就可以用来进行参数更新了。下面讨论参数跟新的几种方法。
SGD and bells and whistles
Vanilla update 最简单的形式就是 沿着负梯度方向更新参数。假设参数向量x,梯度向量dx,形式如下:
# Vanilla update
x += - learning_rate * dx
learning_rate是超参数.如果在整个数据集上进行计算,且learning_rate 足够低的话,这种更新可以保证损失函数是不会上升的。
Momentum update是另外一种几乎总是收敛得更快的更新方法。该方法可以看成是最优化问题从物理角度上得到的启发。损失值可以理解为是丘陵的高度(因为高度势能是U=mgh,所以有\(U\propto h\))。随机初始化参数等同于在某个位置给质点设定为0的初始速度。这样最优化过程可以看做是模拟参数向量(即质点)在地形上滚动的过程。
由于作用在质点上的力量和势能的梯度相关,质点感受到的力就是损失函数的(负)梯度。另外,F=ma,所以,从这个角度看(负)梯度正比于质点的加速度。注意这个理解和上面的随机梯度下降(SDG)是不同的,在普通版本中,梯度直接影响位置。而在这个版本的更新中,物理观点建议梯度只是影响速度,然后速度再影响位置。
动量法有两个版本
第一个版本:
\[v_t = \mu v_{t-1} + \eta \nabla_\theta J( \theta) \\ \theta = \theta - v_t\]第二个版本:
\[v_t = \mu v_{t-1} - \eta \nabla_\theta J( \theta) \\ \theta = \theta + v_t\]cs231n中使用的是第二个版本
# Momentum update
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position
mu在优化中一般称为momentum,一般设置为0.9,但是该变量的物理意义与摩擦系数比较一致,这个变量有效地抑制了速度,降低了系统的动能,不然质点在山底永远不会停下来。在交叉验证中,mu一般设置在[0.5,0.9,0.95,0.99]进行选择。和学习率随着时间退火(下文有讨论)类似,动量有时会提高优化的效果,此时momentum在学习的后期上升。典型的设置是开始时mementum (mu)设置为0.5,然后随着迭代轮数的增加退火至0.99。
通过动量更新,参数向量会在任何有持续梯度的方向上增加速度。
这个可以理解为 “若当前的梯度方向与累积的历史梯度方向一致,则当前的梯度会被加强,从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致,则会减弱当前下降的梯度幅度“
因为动量其实就是历史梯度的加权平均,理解了这一点,动量的物理含义也就比较好理解了。
Nesterov Momentum 是一个稍有不同的动量版本,该方法对凸函数有更强的理论收敛保证,在实际中,该方法也比标准的动量方法效果好一点点。
该方法的主要思想是当当前参数向量在位置x上时 ,观察上面的动量更新公式可以发现, 如果只考虑动量那一项的话,动量部分(忽略第二部分)会把参数向量改变\(mu\ast v\), 因此,当我们计算梯度时,我们可以将未来的近似位置\(x+mu\ast v\) 看做是向前看一步,这个附近的点也是我们将要到达的地方。因为,计算x+mu*v位置的梯度也就比较合理了。
\[\theta_{t-1}' = \theta_{t-1} + \mu v_{t-1} \\ v_t = \mu v_{t-1} - \eta \nabla_\theta J( \theta_{t-1}') \\ \theta_t = \theta_{t-1} + v_t\]#Nesterov Momentum update
x_ahead = x + mu * v
# 计算dx_ahead(在x_ahead处的梯度,而不是在x处的梯度)
v = mu * v - learning_rate * dx_ahead
x += v
但是,实际上人们更喜欢把更新表示为类似于标准的sgd和前面的动量更新的形式,我们可以通过对x_ahead = x + mu * v进行变量转换来实现这个目的。然后用x_ahead而不是x来表示更新。就是说,我们实际存储的其实是向前看一步的参数向量。x_ahead的公式(将其重新命名为x)就变成了:
v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form
令\(\theta_{t-1}' = \theta_{t-1}\)
有
\[\theta_{t}= \theta_{t-1} + \mu^2 v_{t-1} -(1+\mu) \eta \nabla_\theta J( \theta_{t-1})\]CS231n的更新方法是到第4行。
两种动量方法可以从下图中看出区别:

Annealing the learning rate
训练神经网络时,随着时间对学习率退火是有帮助的。要记住的一点是 学习率比较大时,系统中的能量太大,参数向量来回震荡,难以收敛到损失函数更深更窄的部分。知道何时减小学习率是有技巧的,减小慢的话就会浪费计算,很长时间内都来回动荡且没有什么提升。但是减小很快的话系统就会冷却的太快,无法达到最佳的位置。有三种方式实现学习率衰减:
1.Step decay
每隔几轮就将学习率减少一个因子。比较典型的是每5轮将学习率减半,或者每20轮减少0.1.这些值严重依赖模型和问题的类型。实践中你可能见过的启发式做法是使用固定的学习率进行训练时观察验证集误差,当验证集性能停止提升时以一个常数比例降低学习率。
2.Exponential decay
\[\alpha = \alpha_0 e^{-k t}\]\(\alpha_0, k\)是超参数,t是迭代步数,也可以使用epoch作为单位。
3.1/t decay
\[\alpha = \alpha_0 / (1 + k t )\]\(\alpha_0, k\)是超参数,t是迭代步数,
实际应用时,我们发现step decay更受欢迎,因为他的超参数(衰减的比例和以epoch为单位的步数)比超参数k更有解释性。
Second order methods
另外一种比较流行的方法是基于牛顿法:
\[x \leftarrow x - [H f(x)]^{-1} \nabla f(x)\]其中,Hf(x)是Hessian 矩阵,是目标函数的二阶偏导组成的方阵。\(\nabla f(x)\)是梯度向量。直观理解,Hessian矩阵描述了损失函数的局部曲率,允许我们更有效的更新参数。尤其是乘以Hessian 的逆允许我们在大曲率的时候步子较大,小曲率的时候步子较小。更重要的是,这个方法没有学习率这个超参数,这也是支持者们认为该方法相比一阶方法的重要优势。
但是,该方法实际上是不可行的,因为在时间和空间上计算Hessian矩阵的逆都很困难。因此,有很多 quasi-Newton 法可以近似Hessian矩阵的逆 。其中,最流行的是L-BFGS。但是该方法必须在整个训练集上计算,很难用mini-batch的方法进行更新。
现在,实际上很少看到L-BFGS和类似的二阶方法应用到大规模神经网络和CNN中,基于动量的梯度方法更常用。
Per-parameter adaptive learning rate methods
前面的方法对所有的参数都使用相同的学习率。调整学习率代价很大,也已经有很多方法自适应的调整学习率,甚至是每个参数一个学习率。下面介绍几种常用的方法
Adagrad(Adaptive Gradient)
# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)
cache 维度和梯度向量dx相同,每个元素记录了每个参数的历史梯度的平方和。然后在每次更新参数时用来做归一化。可以看出,梯度比较大的参数的梯度会减小,同时,梯度比较小的参数的梯度会增大。有趣的是,平方根操作很重要,如果没有这个操作的话,这个算法的效果会差很多。平滑项eps(通常设置为1e-4到1e-8之间)用来避免除0。Adagrad的一个缺点是,在深度学习中单调的学习率被证明通常过于激进且过早停止学习。
Adagrad的主要思想是”对于出现次数较少的特征,我们对其采用更大的学习率,对于出现次数较多的特征,我们对其采用较小的学习率“ 这个思想和FTRL中对参数的学习率设置是一样的,而且更新形式也很相似。但是,Adagrad有一个缺点,就是随着迭代进行,梯度的平方和越来越大,会导致学习率越来越小,最终无法学习到新的信息。
RMSprop(Root Mean Square Propagation)
该方法很有效,但是并未发表,是 Geoff Hinton在cs321中提到的。RMSprop方法对Adagrad方法做了一个简单的调整,降低了Adagrad激进且单调下降的学习率。具体说来,它使用了平方梯度的移动平均。
cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)
decay_rate 是一个超参数,通常设置为 [0.9, 0.99, 0.999]。RMSProp仍然是基于梯度的大小来对每个权重的学习率进行修改,这同样效果不错。但是和Adagrad不同,其更新不会让学习率单调变小。
Adadelta(adaptive delta)
adadelta 也是为了解决adagrad的学习率单调递减的问题而提出的。该算法和RMSProp基本上是一样的,除了一点,那就是该算法不需要初始学习率。
它提出了两点改进:
一是划定一个窗口,只对该窗口内的历史梯度计算平和和。实现的时候使用移动加权平均,和Rmsprop是一样的。
二是近似海森矩阵的逆,从而摆脱对初始学习率的依赖
\[\Delta x \approx \frac{\frac{\partial f}{\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}=\frac{1}{\frac{\partial^{2}f}{\partial x^{2}}}\cdot g_{t}\] \[\frac{1}{\frac{\partial^{2}f}{\partial x^{2}}}=\frac{\Delta x}{\frac{\partial f}{\partial x}}\approx -\frac{RMS[\Delta x]_{t-1}}{RMS[g]_{t}}\] \[RMS[g]_{t}=\sqrt{E[g^{2}]_{t}+\epsilon } \\ E[g^{2}]_{t}=\rho E[g^{2}]_{t-1}+(1-\rho )g_{t}^{2}\] \[RMS[\Delta x]_{t-1} = \sqrt{E[\Delta x^2]_{t-1} +\epsilon } \\ E[\Delta x^2]_{t-1}=\rho E[\Delta x^2]_{t-2} + (1-\rho)\Delta x_{t-1}^2\]使用\(\Delta x_{t-1}\)是因为\(\Delta x_t\)现在还是未知的。
这个推导过程并没有很理解,可能得看下原论文。
\[\begin{align} \begin{split} \Delta x_t &= - \dfrac{RMS[\Delta x]_{t-1}}{RMS[g]_{t}} g_{t} \\ x_{t+1} &= x_t + \Delta x_t \end{split} \end{align}\]Adam(Adaptive Moment Estimation)
Adam有点像带有动量的RMSProp。
m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)
Adam和RMSprop不同的点在于使用了平滑项m,而不是使用原始梯度向量dx。论文中推荐的值是eps=1e-8,beta1=0.9,beta2=0.999.实践中,Adam现在被推荐为默认算法,通常比RMSprop效果好一点。然而,SGD+Nesterov Momentum 通常也值得一试。完整的Adam更新还包含一个bias correction 机制,因为在前几步中,m、v充分热身之前,m、v 刚被初始化且都都在0附近,这样会导致偏差较大, 因此需要采取一些补偿措施。 加上bias 修正措施之后的Adam如下:
# t is your iteration counter going from 1 to infinity
m = beta1*m + (1-beta1)*dx
mt = m / (1-beta1**t)
v = beta2*v + (1-beta2)*(dx**2)
vt = v / (1-beta2**t)
x += - learning_rate * mt / (np.sqrt(vt) + eps)
Hyperparameter optimization
神经网络中有很多超参数,最常见的有:
学习率
学习率衰减机制(比如使用一个衰减因子)
正则项(L2, dropout)
大型神经网络训练时间会很长,超参数选择花的时间会更久。重要的是要记住这一点,因为这会影响代码库的设计。比如,我们可以设计使用一个worker不断地随机选择超参数并进行优化,在训练过程中,worker会跟踪每个epoch后验证集的效果,并写入到模型checkpoint文件中(包含各种训练指标数据比如随时间变化的logloss),最好是在一个共享文件系统中。把验证集效果直接用在文件名中会比较有用,这样就比较好检查和排序。然后,还有一个master程序,该程序启动或者杀死集群中的worker,也会查看worker写下的checkpoint,输出它们的训练统计数据等。
Prefer one validation fold to cross-validation.
大多数情况下,一个数量较大的验证集会显著简化代码库,不需要使用多个fold进行交叉验证。你可能经常听到人们对一个参数做了交叉验证,但是很多时候他们只使用了一个验证集。
Hyperparameter ranges
在对数尺度上进行超参数搜索。比如,典型的学习率采样方法看起来像这样: learning_rate = 10 ** uniform(-6, 1), 即,我们从一个均匀分布汇总生成一个随机数,然后把它作为10的指数。同样的方法也可以用在正则化项中。直观地说,这是因为学习率和正则化强度都对于训练动态有乘的效果。比如,当学习率只有0.001时,往学习率固定的加0.01对更新过程影响很大。如果是10的话就基本没影响。这是因为学习率是要乘上梯度的。所以,考虑学习率乘以或者除以某个值的一系列数值,比学习率加上或者减去某个值的思路更自然。有一些参数(比如dropout)通常会在原始尺度上进行搜索,比如dropout = uniform(0,1)。
Prefer random search to grid search
randomly chosen trials are more efficient for hyper-parameter optimization than trials on a grid.
Careful with best values on border
有时,有可能你搜索的参数区间是有问题的,比如,我们的学习率搜索空间是 learning_rate = 10 ** uniform(-6, 1),一旦我们获取结果后,我们要检查下最后的学习率不是在区间的边界,否则你可能会错过区间之外的更优的超参数。
Stage your search from coarse to fine
实践中,先从粗糙的范围进行搜索,然后根据最好的结果出现的位置,进一步缩小探索空间。在进行粗略搜索时,可以只跑一个epoch或者更少,因为很多超参数都会让模型什么都学不到,或者损失值突然变得很大。第二步对一个更小的范围进行搜索,这时可以让模型运行5个周期,而最后一个阶段就在最终的范围内进行仔细搜索,运行很多次周期。
Bayesian Hyperparameter Optimization
这个研究领域研究的是如何在超参数空间更有效的搜索。核心思想是在评估不同参数下的模型性能时,在the exploration - exploitation trade-off 中进行权衡。有很多开发了这些模型的超参数工具,比如 Spearmint, SMAC和Hyperopt。然而,在CNN的实践中,这些方法还是比较难以取得比在精心选择的参数区间中进行随机搜索更好的效果。
Evaluation
Model Ensembles
实践中,提高神经网络效果的一个比较可靠的方法就是训练多个独立的模型,测试时对所有模型的估计值进行平均。模型越多,效果越好,只是收益越来越小。ensemble中模型差别越大效果提升越明显。 下面是ensemble的一些方法
**Same model, different initializations. **
Top models discovered during cross-validation
Different checkpoints of a single model
Running average of parameters during training
参考:
1.http://cs231n.github.io/neural-networks-3/
2.http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
3.https://zhuanlan.zhihu.com/p/22810533
4.https://blog.csdn.net/u012328159/article/details/80311892
5.https://upscfever.com/upsc-fever/en/data/deeplearning2/19.html